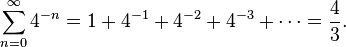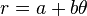Archimedes
Archimedes of Syracuse
(Greek: Ἀρχιμήδης) |
Archimedes Thoughtful by Fetti (1620) |
| Born | c. 287 BC
Syracuse, Sicily
Magna Graecia |
| Died | c. 212 BC (aged around 75)
Syracuse |
| Residence | Syracuse, Sicily |
| Fields | Mathematics, Physics, Engineering, Astronomy, Invention |
| Known for | Archimedes' Principle, Archimedes' screw, Hydrostatics, Levers, Infinitesimals |
Archimedes of Syracuse (
Greek:
Ἀρχιμήδης;
c. 287 BC –
c. 212 BC) was a
Greek mathematician,
physicist,
engineer,
inventor, and
astronomer. Although few details of his life are known, he is regarded as one of the leading
scientists in
classical antiquity. Among his advances in
physics are the foundations of
hydrostatics,
statics and an explanation of the principle of the
lever. He is credited with designing innovative
machines, including siege engines and the
screw pump that bears his name. Modern experiments have tested claims that Archimedes designed machines capable of lifting attacking ships out of the water and setting ships on fire using an array of mirrors.
[1]
Archimedes is generally considered to be the greatest
mathematician of antiquity and one of the greatest of all time.
[2][3] He used the
method of exhaustion to calculate the
area under the arc of a
parabola with the
summation of an infinite series, and gave a remarkably accurate approximation of
pi.
[4] He also defined the
spiral bearing his name, formulae for the
volumes of
surfaces of revolution and an ingenious system for expressing very large numbers.
Archimedes died during the
Siege of Syracuse when he was killed by a
Roman soldier despite orders that he should not be harmed.
Cicero describes visiting the tomb of Archimedes, which was surmounted by a
sphere inscribed within a
cylinder. Archimedes had proven that the sphere has two thirds of the volume and surface area of the cylinder (including the bases of the latter), and regarded this as the greatest of his mathematical achievements.
Unlike his inventions, the mathematical writings of Archimedes were little known in antiquity. Mathematicians from
Alexandria read and quoted him, but the first comprehensive compilation was not made until
c. 530 AD by
Isidore of Miletus, while commentaries on the works of Archimedes written by
Eutocius in the sixth century AD opened them to wider readership for the first time. The relatively few copies of Archimedes' written work that survived through the
Middle Ages were an influential source of ideas for scientists during the
Renaissance,
[5] while the discovery in 1906 of previously unknown works by Archimedes in the
Archimedes Palimpsest has provided new insights into how he obtained mathematical results.
[6]
Biography
Archimedes was born
c. 287 BC in the seaport city of
Syracuse, Sicily, at that time a self-governing
colony in
Magna Graecia. The date of birth is based on a statement by the
Byzantine Greek historian
John Tzetzes that Archimedes lived for 75 years.
[7] In
The Sand Reckoner, Archimedes gives his father's name as Phidias, an
astronomer about whom nothing is known.
Plutarch wrote in his
Parallel Lives that Archimedes was related to King
Hiero II, the ruler of Syracuse.
[8] A biography of Archimedes was written by his friend Heracleides but this work has been lost, leaving the details of his life obscure.
[9] It is unknown, for instance, whether he ever married or had children. During his youth Archimedes may have studied in
Alexandria,
Egypt, where
Conon of Samos and
Eratosthenes of Cyrene were contemporaries. He referred to Conon of Samos as his friend, while two of his works (
The Method of Mechanical Theorems and the
Cattle Problem) have introductions addressed to Eratosthenes.
[a]
Archimedes died
c. 212 BC during the
Second Punic War, when Roman forces under General
Marcus Claudius Marcellus captured the city of Syracuse after a two-year-long
siege. According to the popular account given by
Plutarch, Archimedes was contemplating a
mathematical diagram when the city was captured. A Roman soldier commanded him to come and meet General Marcellus but he declined, saying that he had to finish working on the problem. The soldier was enraged by this, and killed Archimedes with his sword. Plutarch also gives a
lesser-known account of the death of Archimedes which suggests that he may have been killed while attempting to surrender to a Roman soldier. According to this story, Archimedes was carrying mathematical instruments, and was killed because the soldier thought that they were valuable items. General Marcellus was reportedly angered by the death of Archimedes, as he considered him a valuable scientific asset and had ordered that he not be harmed.
[10]
A sphere has 2/3 the volume and surface area of its circumscribing cylinder. A
sphere and
cylinder were placed on the tomb of Archimedes at his request.
The last words attributed to Archimedes are "Do not disturb my circles" (
Greek:
μή μου τούς κύκλους τάραττε), a reference to the circles in the mathematical drawing that he was supposedly studying when disturbed by the Roman soldier. This quote is often given in
Latin as "Noli turbare circulos meos," but there is no reliable evidence that Archimedes uttered these words and they do not appear in the account given by Plutarch.
[10]
The tomb of Archimedes carried a sculpture illustrating his favorite mathematical proof, consisting of a
sphere and a
cylinder of the same height and diameter. Archimedes had proven that the volume and surface area of the sphere are two thirds that of the cylinder including its bases. In 75 BC, 137 years after his death, the Roman
orator Cicero was serving as
quaestor in
Sicily. He had heard stories about the tomb of Archimedes, but none of the locals was able to give him the location. Eventually he found the tomb near the Agrigentine gate in Syracuse, in a neglected condition and overgrown with bushes. Cicero had the tomb cleaned up, and was able to see the carving and read some of the verses that had been added as an inscription.
[11]
The standard versions of the life of Archimedes were written long after his death by the historians of Ancient Rome. The account of the siege of Syracuse given by
Polybius in his
Universal History was written around seventy years after Archimedes' death, and was used subsequently as a source by Plutarch and
Livy. It sheds little light on Archimedes as a person, and focuses on the war machines that he is said to have built in order to defend the city.
[12]
Discoveries and inventions
The Golden Crown
Archimedes may have used his principle of buoyancy to determine whether the golden crown was less
dense than solid gold.
The most widely known
anecdote about Archimedes tells of how he invented a method for determining the volume of an object with an irregular shape. According to
Vitruvius, a
votive crown for a temple had been made for King Hiero II, who had supplied the pure
gold to be used, and Archimedes was asked to determine whether some
silver had been substituted by the dishonest goldsmith.
[13] Archimedes had to solve the problem without damaging the crown, so he could not melt it down into a regularly shaped body in order to calculate its
density. While taking a bath, he noticed that the level of the water in the tub rose as he got in, and realized that this effect could be used to determine the
volume of the crown. For practical purposes water is incompressible,
[14] so the submerged crown would displace an amount of water equal to its own volume. By dividing the mass of the crown by the volume of water displaced, the density of the crown could be obtained. This density would be lower than that of gold if cheaper and less dense metals had been added. Archimedes then took to the streets naked, so excited by his discovery that he had forgotten to dress, crying "
Eureka!" (
Greek: "εὕρηκα!," meaning "I have found it!"). The test was conducted successfully, proving that silver had indeed been mixed in.
[15]
The story of the golden crown does not appear in the known works of Archimedes. Moreover, the practicality of the method it describes has been called into question, due to the extreme accuracy with which one would have to measure the water displacement.
[16] Archimedes may have instead sought a solution that applied the principle known in
hydrostatics as
Archimedes' Principle, which he describes in his treatise
On Floating Bodies. This principle states that a body immersed in a fluid experiences a buoyant force equal to the weight of the fluid it displaces.
[17] Using this principle, it would have been possible to compare the density of the golden crown to that of solid gold by balancing the crown on a scale with a gold reference sample, then immersing the apparatus in water. If the crown was less dense than gold, it would displace more water due to its larger volume, and thus experience a greater buoyant force than the reference sample. This difference in buoyancy would cause the scale to tip accordingly.
Galileo considered it "probable that this method is the same that Archimedes followed, since, besides being very accurate, it is based on demonstrations found by Archimedes himself."
[18]
The Archimedes Screw
A large part of Archimedes' work in engineering arose from fulfilling the needs of his home city of Syracuse. The Greek writer
Athenaeus of Naucratis described how King Hieron II commissioned Archimedes to design a huge ship, the
Syracusia, which could be used for luxury travel, carrying supplies, and as a naval warship. The
Syracusia is said to have been the largest ship built in classical antiquity.
[19] According to Athenaeus, it was capable of carrying 600 people and included garden decorations, a
gymnasium and a temple dedicated to the goddess
Aphrodite among its facilities. Since a ship of this size would leak a considerable amount of water through the hull, the
Archimedes screw was purportedly developed in order to remove the bilge water. Archimedes' machine was a device with a revolving screw-shaped blade inside a cylinder. It was turned by hand, and could also be used to transfer water from a
low-lying body of water into irrigation canals. The Archimedes screw is still in use today for pumping liquids and granulated solids such as coal and grain. The Archimedes screw described in Roman times by
Vitruvius may have been an improvement on a screw pump that was used to irrigate the
Hanging Gardens of Babylon.
[20][21][22]
The Claw of Archimedes
The
Claw of Archimedes is a weapon that he is said to have designed in order to defend the city of Syracuse. Also known as "the ship shaker," the claw consisted of a crane-like arm from which a large metal grappling hook was suspended. When the claw was dropped onto an attacking ship the arm would swing upwards, lifting the ship out of the water and possibly sinking it. There have been modern experiments to test the feasibility of the claw, and in 2005 a television documentary entitled
Superweapons of the Ancient World built a version of the claw and concluded that it was a workable device.
[23][24]
The Archimedes Heat Ray – myth or reality?
The 2nd century AD author
Lucian wrote that during the
Siege of Syracuse (
c. 214–212 BC), Archimedes destroyed enemy ships with fire. Centuries later,
Anthemius of Tralles mentions
burning-glasses as Archimedes' weapon.
[25] The device, sometimes called the "Archimedes heat ray", was used to focus sunlight onto approaching ships, causing them to catch fire.
This purported weapon has been the subject of ongoing debate about its credibility since the Renaissance.
René Descartes rejected it as false, while modern researchers have attempted to recreate the effect using only the means that would have been available to Archimedes.
[26] It has been suggested that a large array of highly polished
bronze or
copper shields acting as mirrors could have been employed to focus sunlight onto a ship. This would have used the principle of the
parabolic reflector in a manner similar to a
solar furnace.
A test of the Archimedes heat ray was carried out in 1973 by the Greek scientist Ioannis Sakkas. The experiment took place at the
Skaramagas naval base outside
Athens. On this occasion 70 mirrors were used, each with a copper coating and a size of around five by three feet (1.5 by 1 m). The mirrors were pointed at a plywood
mock-up of a Roman warship at a distance of around 160 feet (50 m). When the mirrors were focused accurately, the ship burst into flames within a few seconds. The plywood ship had a coating of
tar paint, which may have aided combustion.
[27]
In October 2005 a group of students from the
Massachusetts Institute of Technology carried out an experiment with 127 one-foot (30 cm) square mirror tiles, focused on a
mock-up wooden ship at a range of around 100 feet (30 m). Flames broke out on a patch of the ship, but only after the sky had been cloudless and the ship had remained stationary for around ten minutes. It was concluded that the device was a feasible weapon under these conditions. The MIT group repeated the experiment for the television show
MythBusters, using a wooden fishing boat in
San Francisco as the target. Again some charring occurred, along with a small amount of flame. In order to catch fire, wood needs to reach its
autoignition temperature, which is around 300 °C (570 °F).
[28][29]
When
MythBusters broadcast the result of the San Francisco experiment in January 2006, the claim was placed in the category of "busted" (or failed) because of the length of time and the ideal weather conditions required for combustion to occur. It was also pointed out that since Syracuse faces the sea towards the east, the Roman fleet would have had to attack during the morning for optimal gathering of light by the mirrors.
MythBusters also pointed out that conventional weaponry, such as flaming arrows or bolts from a catapult, would have been a far easier way of setting a ship on fire at short distances.
[1]
Other discoveries and inventions
While Archimedes did not invent the
lever, he gave an explanation of the principle involved in his work
On the Equilibrium of Planes. Earlier descriptions of the lever are found in the
Peripatetic school of the followers of
Aristotle, and are sometimes attributed to
Archytas.
[30][31] According to
Pappus of Alexandria, Archimedes' work on levers caused him to remark: "Give me a place to stand on, and I will move the Earth." (
Greek:
δῶς μοι πᾶ στῶ καὶ τὰν γᾶν κινάσω)
[32] Plutarch describes how Archimedes designed
block-and-tackle pulley systems, allowing sailors to use the principle of
leverage to lift objects that would otherwise have been too heavy to move.
[33] Archimedes has also been credited with improving the power and accuracy of the
catapult, and with inventing the
odometer during the
First Punic War. The odometer was described as a cart with a gear mechanism that dropped a ball into a container after each mile traveled.
[34]
Cicero (106–43 BC) mentions Archimedes briefly in his
dialogue De re publica, which portrays a fictional conversation taking place in 129 BC. After the capture of Syracuse
c. 212 BC, General
Marcus Claudius Marcellus is said to have taken back to Rome two mechanisms used as aids in astronomy, which showed the motion of the Sun, Moon and five planets. Cicero mentions similar mechanisms designed by
Thales of Miletus and
Eudoxus of Cnidus. The dialogue says that Marcellus kept one of the devices as his only personal loot from Syracuse, and donated the other to the Temple of Virtue in Rome. Marcellus' mechanism was demonstrated, according to Cicero, by
Gaius Sulpicius Gallus to
Lucius Furius Philus, who described it thus:
Hanc sphaeram Gallus cum moveret, fiebat ut soli luna totidem conversionibus in aere illo quot diebus in ipso caelo succederet, ex quo et in caelo sphaera solis fieret eadem illa defectio, et incideret luna tum in eam metam quae esset umbra terrae, cum sol e regione. — When Gallus moved the globe, it happened that the Moon followed the Sun by as many turns on that bronze contrivance as in the sky itself, from which also in the sky the Sun's globe became to have that same eclipse, and the Moon came then to that position which was its shadow on the Earth, when the Sun was in line.
[35][36]
This is a description of a
planetarium or
orrery.
Pappus of Alexandria stated that Archimedes had written a manuscript (now lost) on the construction of these mechanisms entitled
On Sphere-Making. Modern research in this area has been focused on the
Antikythera mechanism, another device from classical antiquity that was probably designed for the same purpose. Constructing mechanisms of this kind would have required a sophisticated knowledge of
differential gearing. This was once thought to have been beyond the range of the technology available in ancient times, but the discovery of the Antikythera mechanism in 1902 has confirmed that devices of this kind were known to the ancient Greeks.
[37][38]
Mathematics
While he is often regarded as a designer of mechanical devices, Archimedes also made contributions to the field of mathematics.
Plutarch wrote: "He placed his whole affection and ambition in those purer speculations where there can be no reference to the vulgar needs of life."
[39]
Archimedes was able to use
infinitesimals in a way that is similar to modern
integral calculus. Through proof by contradiction (
reductio ad absurdum), he could give answers to problems to an arbitrary degree of accuracy, while specifying the limits within which the answer lay. This technique is known as the
method of exhaustion, and he employed it to approximate the value of
π (pi). He did this by drawing a larger
polygon outside a
circle and a smaller polygon inside the circle. As the number of sides of the polygon increases, it becomes a more accurate approximation of a circle. When the polygons had 96 sides each, he calculated the lengths of their sides and showed that the value of π lay between 3
1⁄7 (approximately 3.1429) and 3
10⁄71 (approximately 3.1408), consistent with its actual value of approximately 3.1416. He also proved that the
area of a circle was equal to π multiplied by the
square of the
radius of the circle. In
On the Sphere and Cylinder, Archimedes postulates that any magnitude when added to itself enough times will exceed any given magnitude. This is the
Archimedean property of real numbers.
[40]
In
Measurement of a Circle, Archimedes gives the value of the
square root of 3 as lying between
265⁄153 (approximately 1.7320261) and
1351⁄780 (approximately 1.7320512). The actual value is approximately 1.7320508, making this a very accurate estimate. He introduced this result without offering any explanation of the method used to obtain it. This aspect of the work of Archimedes caused
John Wallis to remark that he was: "as it were of set purpose to have covered up the traces of his investigation as if he had grudged posterity the secret of his method of inquiry while he wished to extort from them assent to his results."
[41]
As proven by Archimedes, the area of the
parabolic segment in the upper figure is equal to 4/3 that of the inscribed triangle in the lower figure.
In
The Quadrature of the Parabola, Archimedes proved that the area enclosed by a
parabola and a straight line is
4⁄3 times the area of a corresponding inscribed
triangle as shown in the figure at right. He expressed the solution to the problem as an
infinite geometric series with the
common ratio 1⁄4:
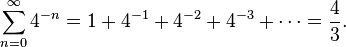
If the first term in this series is the area of the triangle, then the second is the sum of the areas of two triangles whose bases are the two smaller
secant lines, and so on. This proof uses a variation of the series
1/4 + 1/16 + 1/64 + 1/256 + · · · which sums to
1⁄3.
In
The Sand Reckoner, Archimedes set out to calculate the number of grains of sand that the universe could contain. In doing so, he challenged the notion that the number of grains of sand was too large to be counted. He wrote: "There are some, King Gelo (Gelo II, son of
Hiero II), who think that the number of the sand is infinite in multitude; and I mean by the sand not only that which exists about Syracuse and the rest of Sicily but also that which is found in every region whether inhabited or uninhabited." To solve the problem, Archimedes devised a system of counting based on the
myriad. The word is from the Greek
μυριάς murias, for the number 10,000. He proposed a number system using powers of a myriad of myriads (100 million) and concluded that the number of grains of sand required to fill the universe would be 8
vigintillion, or 8 × 10
63.
[42]
Writings
The works of Archimedes were written in
Doric Greek, the dialect of ancient
Syracuse.
[43] The written work of Archimedes has not survived as well as that of
Euclid, and seven of his treatises are known to have existed only through references made to them by other authors.
Pappus of Alexandria mentions
On Sphere-Making and another work on
polyhedra, while
Theon of Alexandria quotes a remark about
refraction from the
now-lost Catoptrica.
[b] During his lifetime, Archimedes made his work known through correspondence with the mathematicians in
Alexandria. The writings of Archimedes were collected by the
Byzantine architect
Isidore of Miletus (
c. 530 AD), while commentaries on the works of Archimedes written by
Eutocius in the sixth century AD helped to bring his work a wider audience. Archimedes' work was translated into Arabic by
Thābit ibn Qurra (836–901 AD), and Latin by
Gerard of Cremona (
c. 1114–1187 AD). During the
Renaissance, the
Editio Princeps (First Edition) was published in
Basel in 1544 by Johann Herwagen with the works of Archimedes in Greek and Latin.
[44] Around the year 1586
Galileo Galilei invented a hydrostatic balance for weighing metals in air and water after apparently being inspired by the work of Archimedes.
[45]
Surviving works
Archimedes is said to have remarked of the
lever:
Give me a place to stand on, and I will move the Earth. - On the Equilibrium of Planes (two volumes)
- The first book is in fifteen propositions with seven postulates, while the second book is in ten propositions. In this work Archimedes explains the Law of the Lever, stating, "Magnitudes are in equilibrium at distances reciprocally proportional to their weights."
- Archimedes uses the principles derived to calculate the areas and centers of gravity of various geometric figures including triangles, parallelograms and parabolas.[46]
- This is a short work consisting of three propositions. It is written in the form of a correspondence with Dositheus of Pelusium, who was a student of Conon of Samos. In Proposition II, Archimedes shows that the value of π (pi) is greater than 223⁄71 and less than 22⁄7. The latter figure was used as an approximation of π throughout the Middle Ages and is still used today when only a rough figure is required.
- This work of 28 propositions is also addressed to Dositheus. The treatise defines what is now called the Archimedean spiral. It is the locus of points corresponding to the locations over time of a point moving away from a fixed point with a constant speed along a line which rotates with constant angular velocity. Equivalently, in polar coordinates (r, θ) it can be described by the equation
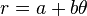
- with real numbers a and b. This is an early example of a mechanical curve (a curve traced by a moving point) considered by a Greek mathematician.
- On the Sphere and the Cylinder (two volumes)
- In this treatise addressed to Dositheus, Archimedes obtains the result of which he was most proud, namely the relationship between a sphere and a circumscribed cylinder of the same height and diameter. The volume is 4⁄3πr3 for the sphere, and 2πr3 for the cylinder. The surface area is 4πr2 for the sphere, and 6πr2 for the cylinder (including its two bases), where r is the radius of the sphere and cylinder. The sphere has a volume two-thirds that of the circumscribed cylinder. Similarly, the sphere has an area two-thirds that of the cylinder (including the bases). A sculpted sphere and cylinder were placed on the tomb of Archimedes at his request.
- This is a work in 32 propositions addressed to Dositheus. In this treatise Archimedes calculates the areas and volumes of sections of cones, spheres, and paraboloids.
- On Floating Bodies (two volumes)
- In the first part of this treatise, Archimedes spells out the law of equilibrium of fluids, and proves that water will adopt a spherical form around a center of gravity. This may have been an attempt at explaining the theory of contemporary Greek astronomers such as Eratosthenes that the Earth is round. The fluids described by Archimedes are not self-gravitating, since he assumes the existence of a point towards which all things fall in order to derive the spherical shape.
- In the second part, he calculates the equilibrium positions of sections of paraboloids. This was probably an idealization of the shapes of ships' hulls. Some of his sections float with the base under water and the summit above water, similar to the way that icebergs float. Archimedes' principle of buoyancy is given in the work, stated as follows:
Any body wholly or partially immersed in a fluid experiences an upthrust equal to, but opposite in sense to, the weight of the fluid displaced.
- In this work of 24 propositions addressed to Dositheus, Archimedes proves by two methods that the area enclosed by a parabola and a straight line is 4/3 multiplied by the area of a triangle with equal base and height. He achieves this by calculating the value of a geometric series that sums to infinity with the ratio 1⁄4.
- This is a dissection puzzle similar to a Tangram, and the treatise describing it was found in more complete form in the Archimedes Palimpsest. Archimedes calculates the areas of the 14 pieces which can be assembled to form a square. Research published by Dr. Reviel Netz of Stanford University in 2003 argued that Archimedes was attempting to determine how many ways the pieces could be assembled into the shape of a square. Dr. Netz calculates that the pieces can be made into a square 17,152 ways.[47] The number of arrangements is 536 when solutions that are equivalent by rotation and reflection have been excluded.[48] The puzzle represents an example of an early problem in combinatorics.
- The origin of the puzzle's name is unclear, and it has been suggested that it is taken from the Ancient Greek word for throat or gullet, stomachos (στόμαχος).[49] Ausonius refers to the puzzle as Ostomachion, a Greek compound word formed from the roots of ὀστέον (osteon, bone) and μάχη (machē – fight). The puzzle is also known as the Loculus of Archimedes or Archimedes' Box.[50]
- This work was discovered by Gotthold Ephraim Lessing in a Greek manuscript consisting of a poem of 44 lines, in the Herzog August Library in Wolfenbüttel, Germany in 1773. It is addressed to Eratosthenes and the mathematicians in Alexandria. Archimedes challenges them to count the numbers of cattle in the Herd of the Sun by solving a number of simultaneous Diophantine equations. There is a more difficult version of the problem in which some of the answers are required to be square numbers. This version of the problem was first solved by A. Amthor[51] in 1880, and the answer is a very large number, approximately 7.760271 × 10206,544.[52]
- In this treatise, Archimedes counts the number of grains of sand that will fit inside the universe. This book mentions the heliocentric theory of the solar system proposed by Aristarchus of Samos, as well as contemporary ideas about the size of the Earth and the distance between various celestial bodies. By using a system of numbers based on powers of the myriad, Archimedes concludes that the number of grains of sand required to fill the universe is 8 × 1063 in modern notation. The introductory letter states that Archimedes' father was an astronomer named Phidias. The Sand Reckoner or Psammites is the only surviving work in which Archimedes discusses his views on astronomy.[53]
- This treatise was thought lost until the discovery of the Archimedes Palimpsest in 1906. In this work Archimedes uses infinitesimals, and shows how breaking up a figure into an infinite number of infinitely small parts can be used to determine its area or volume. Archimedes may have considered this method lacking in formal rigor, so he also used the method of exhaustion to derive the results. As with The Cattle Problem, The Method of Mechanical Theorems was written in the form of a letter to Eratosthenes in Alexandria.
Apocryphal works
Archimedes'
Book of Lemmas or
Liber Assumptorum is a treatise with fifteen propositions on the nature of circles. The earliest known copy of the text is in
Arabic. The scholars
T. L. Heath and
Marshall Clagett argued that it cannot have been written by Archimedes in its current form, since it quotes Archimedes, suggesting modification by another author. The
Lemmas may be based on an earlier work by Archimedes that is now lost.
[54]
It has also been claimed that
Heron's formula for calculating the area of a triangle from the length of its sides was known to Archimedes.
[c] However, the first reliable reference to the formula is given by
Heron of Alexandria in the 1st century AD.
[55]
Archimedes Palimpsest
The foremost document containing the work of Archimedes is the
Archimedes Palimpsest. In 1906, the Danish professor
Johan Ludvig Heiberg visited
Constantinople and examined a 174-page goatskin parchment of prayers written in the 13th century AD. He discovered that it was a
palimpsest, a document with text that had been written over an erased older work. Palimpsests were created by scraping the ink from existing works and reusing them, which was a common practice in the Middle Ages as
vellum was expensive. The older works in the palimpsest were identified by scholars as 10th century AD copies of previously unknown treatises by Archimedes.
[56] The parchment spent hundreds of years in a monastery library in Constantinople before being sold to a private collector in the 1920s. On October 29, 1998 it was sold at auction to an anonymous buyer for $2 million at
Christie's in
New York.
[57] The palimpsest holds seven treatises, including the only surviving copy of
On Floating Bodies in the original Greek. It is the only known source of
The Method of Mechanical Theorems, referred to by Suidas and thought to have been lost forever.
Stomachion was also discovered in the palimpsest, with a more complete analysis of the puzzle than had been found in previous texts. The palimpsest is now stored at the
Walters Art Museum in
Baltimore,
Maryland, where it has been subjected to a range of modern tests including the use of
ultraviolet and
x-ray light to read the overwritten text.
[58]
The treatises in the Archimedes Palimpsest are:
On the Equilibrium of Planes, On Spirals, Measurement of a Circle, On the Sphere and the Cylinder, On Floating Bodies, The Method of Mechanical Theorems and
Stomachion.
Legacy
There is a
crater on the
Moon named
Archimedes (29.7° N, 4.0° W) in his honor, as well as a lunar mountain range, the
Montes Archimedes (25.3° N, 4.6° W).
[59]
The
asteroid 3600 Archimedes is named after him.
[60]
The
Fields Medal for outstanding achievement in mathematics carries a portrait of Archimedes, along with his proof concerning the sphere and the cylinder. The inscription around the head of Archimedes is a quote attributed to him which reads in Latin: "Transire suum pectus mundoque potiri" (Rise above oneself and grasp the world).
[61]
Archimedes has appeared on postage stamps issued by
East Germany (1973),
Greece (1983),
Italy (1983),
Nicaragua (1971),
San Marino (1982), and
Spain (1963).
[62]
The exclamation of
Eureka! attributed to Archimedes is the state motto of
California. In this instance the word refers to the discovery of gold near
Sutter's Mill in 1848 which sparked the
California Gold Rush.
[63]
A movement for civic engagement targeting universal access to health care in the US state of
Oregon has been named the "Archimedes Movement," headed by former Oregon Governor
John Kitzhaber.
[64]
Oktovianus Maniani, right, vies for the ball with Laos player Kitsada in an AFF Cup group stage match in Jakarta. The Merah Putih midfielder is one of the team’s playmakers. AFP Photo 
Albert Einstein was born at Ulm, in Württemberg, Germany, on March 14, 1879. Six weeks later the family moved to Munich, where he later on began his schooling at the Luitpold Gymnasium. Later, they moved to Italy and Albert continued his education at Aarau, Switzerland and in 1896 he entered the Swiss Federal Polytechnic School in Zurich to be trained as a teacher in physics and mathematics. In 1901, the year he gained his diploma, he acquired Swiss citizenship and, as he was unable to find a teaching post, he accepted a position as technical assistant in the Swiss Patent Office. In 1905 he obtained his doctor's degree.
Pengantar 
sumbu dicelupkan dalam wadah yang berisi minyak tanah, sedangkan sebagian lagi dibungkus dalam pipa kecil. Pada ujung atas pipa tersebut, disisakan sebagian sumbu. Jika kita ingin menggunakan lampu minyak, maka sumbu yang terletak di ujung atas pipa kecil tersebut harus dibakar. Sumbu tersebut bisa menyala dalam waktu yang lama karena minyak tanah yang berada dalam wadah merembes ke atas, hingga mencapai ujung sumbu yang terbakar. Aneh ya, kok minyak tanah bisa merembes ke atas ?
rumus lagi, rumus lagi… Untuk membantu kita menurunkan persamaan, perhatikan gambar di bawah.
bagaimana prinsip kerja dongkrak hidrolis ? mobil yang begitu berat bisa diangkat dengan mudah. Aneh bin ajaib. Hehe… semuanya karena fisika. Selain itu, ketika dirimu menumpang mobil atau angkot, coba amati bagaimana kendaraan bisa direm. Kalau pingin iseng, silahkan bertanya kepada om sopir. Om, kok mobilnya bisa berhenti ya ? prinsip kerja rem bagaimana-kah ? mudah2an dirimu tidak diomelin oleh om sopir.
